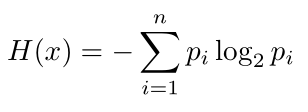Muitas interpretações foram feitas sobre a entropia de algo, mas em imagens, o que significa?
Esse post é uma tradução direta de outro publicado anteriormente em inglês aqui mesmo em meu blog. Optei por uma tradução, já que além de ser um assunto que muito me interessa, gostaria de remover uma possível barreira linguística. Também estou trazendo um carinho adicional para o programa que utilizo para avaliar entropia em imagens: O Cake Image Analyzer.
Claude Shannon nos apresentou em 1948 à Entropia da Informação. Desde então, muitas interpretações foram feitas sobre o valor da entropia de algo, mas ao lidar com imagens, o que significa Entropia? Alguns trabalhos verificaram que a entropia de uma imagem pode ser usada, por exemplo, para medir seus aspectos visuais (Tsai, Lee e Matsuyama, 2008) ou para coletar informações para serem usadas como parâmetros em alguns sistemas (Min et al., 2013 ). Outra interpretação amplamente usada seria para medir a quantidade de informação dentro de uma imagem.
Imagine uma imagem de 1920×1080 com 10.000 pontos coloridos e outra com apenas 5 pontos cinzas. É fácil sabermos qual deles possui mais informações visuais, porém, para o computador, essa não é uma tarefa trivial. Bem, seria, se não tivéssemos a equação da entropia.
Equação
É possível calcular a entropia H(x) usando a seguinte equação:
O valor de pi é a probabilidade de ocorrência de um determinado símbolo. Aqui, os símbolos são pixels. Para simplificar, vamos considerar uma imagem de 8 bits de canal único. Ou seja, 256 níveis de intensidade ( uma imagem tons de cinza para simplificar). Com isso, podemos calcular o valor de pi da seguinte forma:

Codando a Entropia
Primeiro, precisamos de algo para representar o número de ocorrências de cada valor de intensidade. Em outras palavras, precisamos do histograma da imagem. Optei pelo uso da linguagem Java, o motivo que explico no final desta postagem.
A função buildHistogram abaixo é responsável por calcular o histograma:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | /* Create a array of ints, representing the histogram of a given image * @param BufferedImage originalImage - The image to be processed * @param int numberOfBins - Number of histogram bins * @return int bins[] - The array containing the occurrence of each intensity pixel (the histogram) */ public static int[] buildHistogram(BufferedImage image, int numberOfBins){ int bins[]=new int[numberOfBins]; int intensity ; image=getGrayScale8bits(image); for (int i = 0 ; i <= image.getWidth()-1 ; i++){ for (int j=0 ;j <= image.getHeight()-1 ; j++){ intensity = image.getRGB(i,j) & 0xFF; bins[intensity]++; } } return bins; } |
Agora é possível calcular a probabilidade de ocorrência de cada valor de intensidade, mergulhando cada valor da matriz bin[] pelo número de intensidades. Isso é feito no trecho abaixo, que também calcula a entropia.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | /* Compute the entropy of an image based on the Shannon's Formula * @param BufferedImage originalImage - The image to be processed * @param int maxValue - The maximum value of intensity pixels, the same number as the histogram bins * @return int entropyValue - The entropy value */ public static double getEntropy(BufferedImage image, int maxValue){ int bins[] = buildHistogram(image,maxValue); double entropyValue = 0,temp=0; double totalSize = image.getHeight() * image.getWidth(); //total size of all symbols in an image for(int i=0;i<maxValue;i++){ //the number of times a sybmol has occured if(bins[i]>0){ //log of zero goes to infinity temp=(bins[i]/totalSize)*(Math.log(bins[i]/totalSize)); entropyValue += temp; } } return entropyValue*(-1); } |
A soma da equação é feita em um loop For que vai de 0 ao tamanho do histograma. A linha: temp=(bins[i]/totalSize)*(Math.log(bins[i]/totalSize)); calcula pi que é somado na variável entropyValue . A função retorna entropyValue multiplicado por (-1), completando a equação.
Cake image analyzer
Todo o código acima veio de um pequeno programa chamado Cake Image Analyzer que fiz há algum tempo para ajudar as pessoas a ver o valor da entropia de uma imagem.
Para mudar um pouco e, visto que tenho me prendido muito em C++ e Python, usei Java. Em especial a classe BufferedImage, portanto, nenhuma biblioteca adicional foi usada.
Screenshots e Exemplos do Cake
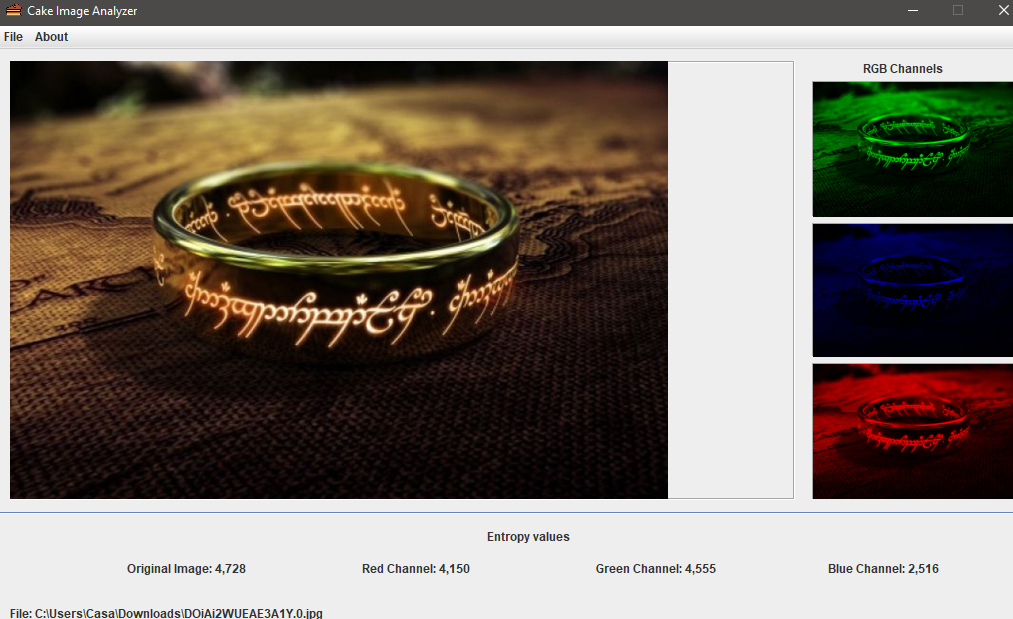
Figura 1 – Imagem com um H(x) de 4.72
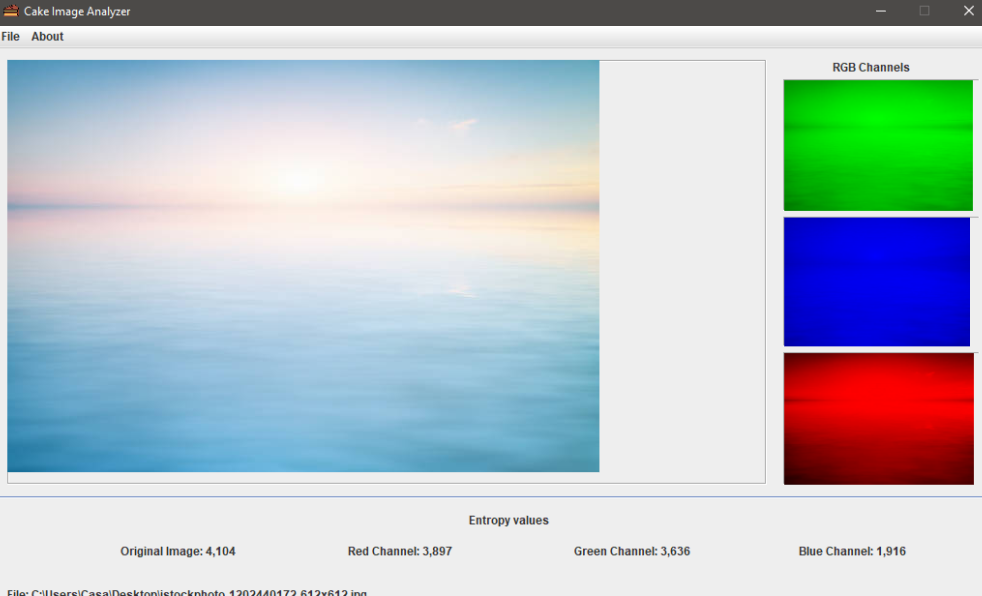
Figura 2 – Imagem com H(x) de 4.1
Como podemos ver, a primeira imagem tem um valor de entropia maior que a segunda. Em outras palavras, poderíamos dizer que ele contém mais informações. E uma imagem contendo apenas pixels da mesma intensidade?
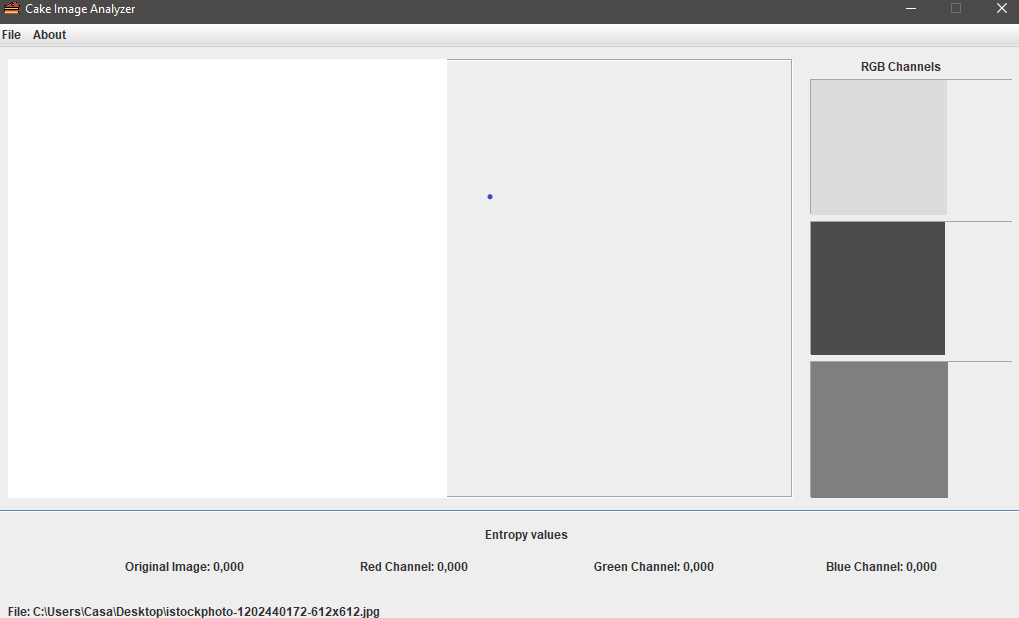
Figura 3 – Imagem com H(x) = 0
Zero, a Figura 3 mostrou uma imagem sem variação, informação e sem desordem. Tudo conforme o planejado pela interpretação de Entropia.
Onde encontro o Cake Image Analyzer?
O código está disponível na minha página do GitHub como de costume. Se você quiser apenas baixar o executável para usar em suas imagens, acesse a página de Releases.
Divirta-se!
Se esse post te ajudou, considere contribuir com um cafézinho!🙂